Das Verfahren Wahrheitstafeln für aussagenlogische Formeln aufzustellen,
sollte aus den Grundvorlesungen bekannt sein. Eine Wahrheitstafel hat
insgesamt soviel Spalten wie es unterschiedliche Variablen gibt plus der
Anzahl aller auftretenden Junktoren. Eine Wahrheitstafel hat bekanntlich
Zeilen, wobei 
die Anzahl der unterschiedlichen Variablen ist. Zusätzlich gibt es noch
eine Kopfzeile, die die Spalten bezeichnet. Auch dieser Beweiser soll
wieder einen String, der als Eingabe für 
benützt werden kann
ausgeben.
Das entsprechende Format, um eine Tabelle in auszugeben, ist die
tabular-Umgebung. Es wird ein Beispiel gegeben, wie eine solche
Tabelle aussehen könnte:
\begin{tabular}{|c|c|c||c|c|c|}\hline
A&B&C&A$\rightarrow$C&$\neg($A$\rightarrow$C)&
$(\neg$(A$\rightarrow$C))$\vee$B\\ \hline\hline
0&0&0&1&0&0\\ \hline
0&0&1&1&0&1\\ \hline
0&1&0&1&0&0\\ \hline
0&1&1&1&0&1\\ \hline
1&0&0&0&1&1\\ \hline
1&0&1&0&1&1\\ \hline
1&1&0&1&0&0\\ \hline
1&1&1&1&0&1\\ \hline
\end{tabular}\\ [1ex]
Die Formel ist keine Tautologie.\\
Wir haben diesmal den Text zur besseren Lesbarkeit nicht mit den
Escape-Sequenzen von Gofer ausgeschrieben. Dieses mubei der
Programmierung natürlich wieder berücksichtigt werden.
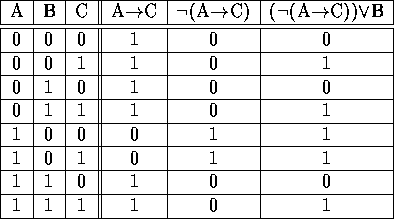
Die Formel ist keine Tautologie.