Der Resolutionsbeweiser

Ein Resolutionsbeweiser generiert aus einer Menge von Klauseln solange neue Klauseln über die Resolution, bis er die leere Klausel erzeugt hat. Damit war sein Beweis erfolgreich. Ein Resolutionsschritt ist ein Ableitungsschritt, in dem aus zwei Klauseln eine neue Klausel generiert wird. Wir definieren diesen Ableitungsschritt:
Definition (Resolution)
Es seien C, C und C Klauseln. C heiResolvente von C, C, wenn es ein Atom p gibt mit

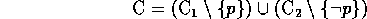
C ensteht dann durch Resolution bzgl. p aus C,C.
Es ist nun der Kalkül vollständig spezifiziert. Eine Regel zur Faktorisierung wird nicht benötigt, da wir uns in der Aussagenlogik befinden und davon ausgehen, dakein Element doppelt in einer Klausel ist. Um einen Resolutionsschritt zu implementieren, ist es notwendig die Vereinigung von Mengen in Gofer zu definieren.
Der Resolutionsbeweiser soll nun eine Klauselmenge nehmen und solange neue Klauseln aus dieser Menge generieren bis entweder die leere Klausel abgeleitet wurde, oder keine neue Klausel mehr erzeugt werden kann. Hierzu munatürlich verhindert werden, daman zwei Klauseln mehrfach auf demselben Literalen resolviert.
Als Ausgabe soll der Beweiser einen String im -Format erzeugen, der den Resolutionsbeweis darstellt. Hier sei den Programmierern ein wenig Freiheit gelassen. Als Beispiel betrachte man folgende Ausgabe:

\\ documentstyle[german]{article}\n\\ begin{document}\nDie Eingabe
klauseln waren:\\ \\ \n\\ {$\\ neg$ A,C\\ }\\ \\ \n\\ {A,$\\ neg$ B\\ }\\ \
\\ n\\ {B,$\\ neg$ C\\ }\\ \\ \n In der n"achsten Iterationsstufe wurd
en als neue Klauseln erzeugt:\\ \\ \n \\ {C,$\\ neg$ B\\ }\\ \\ \n\\ {A,
$\\ neg$ C\\ }\\ \\ \n\\ {A,B\\ }\\ \\ nIn der n"achsten Iterationsstufe
 wurden als neue Klauseln erzeugt:\\ \\ \n

In dieser Iterationsstufe wurde die leere Klausel hergeleitet. D
er Beweis war erfolgreich.\\ end{document}