Der Tableauxbeweiser



Next: Aufgabe 2
Up: Aufgabe 1
Previous: Beweiser über Wahrheitstafeln
Wir beschränken uns in dieser Aufgabe auf Formeln mit den Junktoren
 und
und  . Formeln, die auch den Junktor
. Formeln, die auch den Junktor
 enthalten, müssen zunächst umgeformt werden, was
aber nicht Teil der Aufgabe zu sein braucht.
enthalten, müssen zunächst umgeformt werden, was
aber nicht Teil der Aufgabe zu sein braucht.
Der Tableaukalkül hat als Eigenschaft, daer nicht wie die Resolution
auf Klauseln operiert sondern auf den Formel in ihrer ursprünglichen
Syntax. Tableaubeweise sind damit nicht auf einer so maschinennahen
abstrakten Ebene und für Menschen leichter lesbar.
Der Kalkül operiert auf markierten
Formeln. Eine markierte Formel ist von der Gestalt 0A oder 1A mit A . (Man kann den Tableaukalkül auch auf unmarkierten Formeln
definieren. Die Marken dienen nur der Übersichtlichkeit.)
Wir unterscheiden drei verschiedene Typen markierter Formeln:
. (Man kann den Tableaukalkül auch auf unmarkierten Formeln
definieren. Die Marken dienen nur der Übersichtlichkeit.)
Wir unterscheiden drei verschiedene Typen markierter Formeln:
- Typ
 (elementarer Typ):
(elementarer Typ):  für
für  .
.
- Typ
 (konjunktiver Typ):
(konjunktiver Typ):

- Typ
 (disjunktiver Typ):
(disjunktiver Typ):

Zu jeder nicht elementaren markierten Formel X definieren wir jetzt bis
zu zwei
direkte Abkömmlinge X ,X
,X , gemäfolgender Tabellen:
, gemäfolgender Tabellen:
Typ  Typ
Typ 
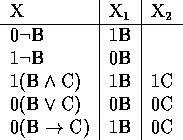
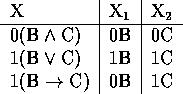
Definition (Tableaux)
Der Tableaukalkül findet sich dargestellt in [].
Es sei E eine endliche Menge von markierten Formeln. Ein Tableau
für E ist ein Binärbaum mit Beschriftung der Knoten durch markierte
Formeln oder durch das Zeichen *, gemäder folgenden rekursiven Definition:
- (1)
- Ist E={X
 X
X }, so ist
}, so ist
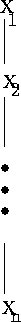
ein Tableau für E.
- (2)
- Ist T ein Tableau für E und
 ein Pfad von der Wurzel zu
einem Blatt, der nirgends mit
* markiert ist (offener Pfad) und auf dem ein Knoten mit X vom Typ
ein Pfad von der Wurzel zu
einem Blatt, der nirgends mit
* markiert ist (offener Pfad) und auf dem ein Knoten mit X vom Typ
 markiert ist;
dann ist auch T' ein Tableau für E, welches durch Verlängern von
markiert ist;
dann ist auch T' ein Tableau für E, welches durch Verlängern von
 um ein Blatt mit der Markierung X
um ein Blatt mit der Markierung X oder X
oder X ensteht.
ensteht.
- (3)
- Ist T ein Tableau für E und
 ein offener Pfad von der
Wurzel zu
einem Blatt, auf dem ein Knoten mit X vom Typ
ein offener Pfad von der
Wurzel zu
einem Blatt, auf dem ein Knoten mit X vom Typ
 markiert ist; dann ist auch T' ein Tableau für E, welches durch
Anhängen zweier Kanten an
markiert ist; dann ist auch T' ein Tableau für E, welches durch
Anhängen zweier Kanten an  zu neuen Blättern mit den Markierungen
X
zu neuen Blättern mit den Markierungen
X und X
und X ensteht.
ensteht.
- (4)
- Ist T ein Tableau für E und
 ein offener Pfad von der
Wurzel zu
einem Blatt, auf dem je ein Knoten mit 0A bzw 1A für A
ein offener Pfad von der
Wurzel zu
einem Blatt, auf dem je ein Knoten mit 0A bzw 1A für A markiert
ist; dann ist auch T' ein Tableau für E, welches durch
Anhängen des neuen Blattes mit der Markierung * an an
markiert
ist; dann ist auch T' ein Tableau für E, welches durch
Anhängen des neuen Blattes mit der Markierung * an an  entsteht.
entsteht.
- (5)
- Nur die gemä(1)-(4) gebildeten Bäume sind Tableaux für E.
Ein Beweis für die allgemeingültigkeit einer Formel F ist ein Tableau
für {0F},dessen Blätter alle mit *
markiert sind.
Aufgabe ist es nun für eine eingegebene Formel F einen Beweis zu führen:
sprich es soll versucht werden, ein Tableaux für 0F zu erstellen, das
entweder nur mit * markierte Blätter besitzt (erfolgreicher Beweis), oder
in dem für jeden
Knoten Knoten auf jeden Pfad durch diesen Knoten die direkten
Abkömmlinge gebildet wurden. Hauptüberlegung ist dabei, eine geeignete
Datenstruktur für Tableaux zu definieren. Es bieten sich dabei mehrere
Alternativen an, zB:
- ein Typ aus zwei Konstruktoren: einer für ein leeres Tableau,
einer für einen Knoten mit seinen beiden Nachfolgern und seiner
Markierung als Argumente. Ein Blatt wäre dann ein Knoten mit nur leeren
Tableaux als Nachfolger.
- ein Typ aus zwei Konstruktoren: einer für ein Blatt und einer
für Knoten mit Nachfolgern.
- ein Typ aus drei Konstruktoren: einer für Blätter (0 Söhne),
einer für Knoten mit einem Sohn und einer für Knoten mit zwei
Söhnen.
Es empfielt sich einem Knoten die Information mitzugeben, ob seine
Abkömmlinge schon vollständig gebildet wurden.
Desweiteren muentschieden werden, nach welcher Strategie die Regeln
zur Bildung des Tableaus angewendet werden. Hierbei muinsbesondere
überlegt werden, wann und wie man prüft, ob ein Pfad mit einem *
abgeschlossen werden darf.
Es wird in dieser Aufgabe keine Ausgabe in  -Format verlangt. Die
Ausgabe des internen Datentypen oder zumindest eine einfache
ASCII-Darstellung eines Tableaus soll reichen. (wobei eine ASCII
Darstellung in Hinblick auf die nächste Aufgabe schöner wäre.)
(Profis ist es natürlich nicht verboten, eine Darstellung im
-Format verlangt. Die
Ausgabe des internen Datentypen oder zumindest eine einfache
ASCII-Darstellung eines Tableaus soll reichen. (wobei eine ASCII
Darstellung in Hinblick auf die nächste Aufgabe schöner wäre.)
(Profis ist es natürlich nicht verboten, eine Darstellung im  -Format zu generieren.)
-Format zu generieren.)



Next: Aufgabe 2
Up: Aufgabe 1
Previous: Beweiser über Wahrheitstafeln
Sven Eric Panitz
Mi., 01. Nov. 1995, 12:12:54
 und
und  . Formeln, die auch den Junktor
. Formeln, die auch den Junktor
 enthalten, müssen zunächst umgeformt werden, was
aber nicht Teil der Aufgabe zu sein braucht.
enthalten, müssen zunächst umgeformt werden, was
aber nicht Teil der Aufgabe zu sein braucht. . (Man kann den Tableaukalkül auch auf unmarkierten Formeln
definieren. Die Marken dienen nur der Übersichtlichkeit.)
Wir unterscheiden drei verschiedene Typen markierter Formeln:
. (Man kann den Tableaukalkül auch auf unmarkierten Formeln
definieren. Die Marken dienen nur der Übersichtlichkeit.)
Wir unterscheiden drei verschiedene Typen markierter Formeln:
 (elementarer Typ):
(elementarer Typ):  für
für  .
.
 (konjunktiver Typ):
(konjunktiver Typ):

 (disjunktiver Typ):
(disjunktiver Typ):

 ,X
,X , gemäfolgender Tabellen:
, gemäfolgender Tabellen: Typ
Typ 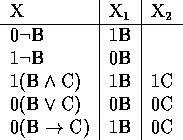
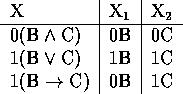
 X
X }, so ist
}, so ist 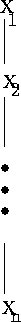
 ein Pfad von der Wurzel zu
einem Blatt, der nirgends mit
* markiert ist (offener Pfad) und auf dem ein Knoten mit X vom Typ
ein Pfad von der Wurzel zu
einem Blatt, der nirgends mit
* markiert ist (offener Pfad) und auf dem ein Knoten mit X vom Typ
 markiert ist;
dann ist auch T' ein Tableau für E, welches durch Verlängern von
markiert ist;
dann ist auch T' ein Tableau für E, welches durch Verlängern von
 markiert
ist; dann ist auch T' ein Tableau für E, welches durch
Anhängen des neuen Blattes mit der Markierung * an an
markiert
ist; dann ist auch T' ein Tableau für E, welches durch
Anhängen des neuen Blattes mit der Markierung * an an  -Format verlangt. Die
Ausgabe des internen Datentypen oder zumindest eine einfache
ASCII-Darstellung eines Tableaus soll reichen. (wobei eine ASCII
Darstellung in Hinblick auf die nächste Aufgabe schöner wäre.)
(Profis ist es natürlich nicht verboten, eine Darstellung im
-Format verlangt. Die
Ausgabe des internen Datentypen oder zumindest eine einfache
ASCII-Darstellung eines Tableaus soll reichen. (wobei eine ASCII
Darstellung in Hinblick auf die nächste Aufgabe schöner wäre.)
(Profis ist es natürlich nicht verboten, eine Darstellung im