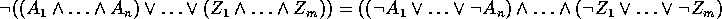
Der Resolutionskalkül arbeitet nicht auf Formeln in ihrer vollen Syntax, wie sie oben definiert sind, sondern auf Klauseln. Klauseln sind hierbei Mengen von Literalen, die implizit disjunktiv verknüpft sind. Ein Literal ist ein Atom oder das Negat eines Atoms. Eine Menge von Klauseln repräsentiert die konjunktive Verknüpfung dieser Disjunktionen, also die konjunktive Normalform einer Formel. Da aber der Resolutionskalkül auf dem Negat einer Formel operiert und versucht einen Widerspruch herzuleiten, erstellen wir von der zu beweisenden Formel die disjunktive Normalform, deren Negat sich dann direkt in eine Klauselform überführen lä. Man mache sich das an folgender schematischen Gleichung deutlich:
Für unsere Zwecke braucht zum Beweis der Allgemeingültigkeit, die
Formel gar nicht negiert zu werden. Wir erstellen einfach die
disjunktive Normalform und schreiben diese als Klauseln. Gegenüber der
Klauselform der negierten Formel ist jedes Literal negiert; damit
können aber genau diesselben Resolutionsschritte durchgeführt werden,
wie auf den Klauseln des Negats der Formel.
Um von einer Formel die disjunktive Normalform zu berechnen, müssen auf
ihr so lange wie möglich die Regeln von folgenden Termersetzungssystem
angewendet werden:
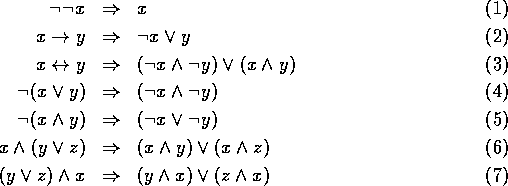
So wie wir es auch gewohnt sind, Klauseln auf dem Papier nicht mehr in der Syntax aussagenlogischer Formeln zu schreiben, sondern als Mengen, werden wir für diese Normalform von Formeln auch einen eigenen Datentypen definieren. Für die Darstellung von Mengen könnte man sich einen eigenen Datentypen definieren. Wir können aber auch auch auf den eingebauten Typ von Listen mit seiner bequemen Syntax zurückgreifen: Eine Klausel ist dann eine Liste von Literalen und eine Formel eine Liste von Klauseln.
>data Literal a = Pos a| > Neg a >type Klausel a = [Literal a] >type NormForm a = [Klausel a] >type LiteralS = Literal String >type KlauselS = Klausel String >type NormFormS = NormForm StringAuch hier haben wir wieder zunächst polymorphe Typen definiert, die wir dann mit Strings instanziiert haben.
>k1 = [[Pos "A", Neg "A", Pos "B"]]Bei der Darstellung von Mengen als Listen ergibt sich eine bekannte Schwierigkeit: In Listen kann es Doppelvorkommen von Elementen geben, was in Mengen nicht erlaubt ist. Eine Möglichkeit diese Doppelvorkommen zu vermeiden, ist, beim Einfügen eines Elementes erst zu überprufen, ob es in der Menge schon enthalten ist. Wir brauchen also spezielle Operationen auf den Listen, die uns die gewünschte Eigenschaft für Mengen geben. Exemplarisch sei hier eine Einfügefunktion für Klauseln angegeben:
>infixr 5 `i` >i :: (Eq a) => a -> [a] -> [a] >i a [] = [a] >i a (x:xs) > |(a==x) = (x:xs) > |otherwise = x:(a `i` xs)Wir haben hiermit eine Infixfunktion definiert, die in eine Liste über einem Typen der Gleichheitsklasse Eq, ein Element hinten einfügt, sofern es noch nicht in der Liste enthalten ist. Um diese Funktion auch auf Klauseln anwenden zu können, müssen wir die Gleichheit auf Literalen definieren. Literale sollen also auch zur Gleichheitsklasse gehören:
>instance (Eq a) => Eq (Literal a) where > (Pos _)==(Neg _) = False > (Neg _)==(Pos _) = False > (Pos a)==(Pos b) = a==b > (Neg a)==(Neg b) = a==bEin Beispielaufruf für unsere Funktion ist:
? (Pos "C") `i` (head k1) [Pos "A", Neg "A", Pos "B", Pos "C"] (31 reductions, 109 cells)Um diese überladene Funktion auch zum Einfügen von Klauseln in eine Klauselmenge zu benutzen, mudie Gleichheit auf Klauseln definiert werden. Da Klauseln Mengen sind, ist es allgemeiner eine Gleichheit auf Listen zu definieren. Diese soll zur Übung von allen Gruppen definiert werden.